Berikut ini, saya berikan 12 nomor soal matematika plus penyelesaiannya tentang komposisi fungsi dan invers fungsi yang dipelajari pada jenjang SMA.
Sebelum berlatih mengerjakan 12 soal di bawah, Gengs dapat mempelajari materi singkatnya DISINI.
Soal 1
Diketahui f(x) = 2x + 15 dan g(x)=4/(x+5); x # -5. Rumus komposisi fungsi (f o g)(x) adalah…
Jawab:
(f o g)(x) = f(g(x))
Jadi, rumus komposisi fungsi (f o g)( x) adalah (15x + 83)/(x + 5)
Soal 2
Diketahui fungsi f(x) = (x + 5)/(x² + 3x – 1) dan g(x) = px – 2. Jika (f o g)(1) = 2, nilai p adalah…
Jawab:
(f o g)(x) = f(g(x))
= f( px – 2)
Pada soal telah diketahui (f o g)(1) = 2 maka substitusikan x = 1, dengan demikian:
(f o g)(1) = [p + 3]/[p² – p -3]
2 = (p + 3)/(p² – p -3)
2(p² – p – 3) = p + 3
2p² – 2p – 6 = p + 3
2p² – 2p – p – 6 – 3 = 0
2p² – 3p – 9 = 0
(2p + 3) (p – 3) = 0
2p + 3 = 0
2p = -3
p = -3/2 atau
p – 3 = 0
p = 3
Jadi, nilai p adalah -3/2 atau 3
Soal 3
Jika g(x) = x + 6 dan (f o g)(x) = 2 √(3x + 19)/(x + 4), rumus fungsi f adalah…
Jawab:
(f o g)(x) = 2 √(3x + 19)/(x + 4)
f(g(x)) = 2 √(3x + 19)/(x + 4)
f(x + 6) = 2 √(3x + 19)/(x + 4)
Misalkan t = x + 6 sehingga x = t – 6
f(x + 6) = 2 √(3x + 19)/(x + 4)
f(t) = 2 √(3(t – 6) + 19)/((t – 6) + 4)
f(t) = 2 √(3t + 1)/(t – 2)
Diperoleh f(x) = 2 √(3x + 1)/(x – 2)
Jadi, rumus fungsi f adalah f(x) = 2 √(3x + 1)/(x – 2)
Soal 4
Diketahui f(x) = mx – 4 dan g(x) = (x – 2)/(x² + x – 1). Jika (f o g)(-1) = 11, nilai m adalah…
Jawab:
(f o g)(x) = f(g(x))
= f((x – 2)/(x² + x – 1))
= m((x – 2)/(x² + x – 1)) – 4
= [m (x – 2)/(x² + x – 1)] – 4[(x² + x – 1)/(x² + x – 1)]
= [m (x – 2) – 4(x² + x- 1)]/(x² + x – 1)
Pada soal diberikan (f o g)(-1) = 11 maka :
(f o g)(-1) = 11
[m (-1 – 2) – 4(-1² + (-1) – 1)]/(-1² + (-1) – 1) = 11
((-3m + 4)/-1) = 11
-3m + 4 = -11
-3m = -15
m = 5
Jadi, nilai m yaitu 5.
Pelajari Juga: 15 Soal Fungsi Komposisi Beserta Jawabannya
Soal 5
Diketahui f(x) = (2x – 1)/(3x + 5); x # -5/3. Rumus invers fungsi f adalah….
Jawab:
Misalkan: y = f(x)
y = (2x – 1)/(3x + 5)
y(3x + 5) = 2x – 1
3xy + 5y = 2x – 1
3xy – 2x = -5y – 1
x(3y – 2) = -5y – 1
x = (-5y – 1)/(3y – 2)
f¯¹(y) = (-5y – 1)/(3y – 2)
f¯¹(x) = (-5x – 1)/(3x -2)
Jadi, rumus invers fungsi f yaitu f¯¹(x) = (-5x – 1)/(3x – 2)
Soal 6
Diketahui f(x) = √(-5x + 4) untuk x ≤ 4/5. Jika f¯¹(x) adalah invers fungsi f, nilai f¯¹(3) adalah…
Jawab:
Pertama-tama akan kita cari f¯¹
Kita akan misalkan y = f(x), dengan demikian:
y = √(-5x + 4)
Kita akan menghilangkan akarnya dengan mengkuadratkan ruas kanan dan ruas kiri.
y² = -5x + 4
5x = 4 – y²
x = (4 – y²)/5
f¯¹(y) = (4 – y²)/5
f¯¹(x) = (4 – x²)/5
Setelah kita peroleh f¯¹(x) selanjutnya akan kita cari f¯¹(3) dengan mensubstitusikan x = 3.
f¯¹(x) = (4 – x²)/5
f¯¹(x) = (4 – 3²)/5 = -5/5 = -1
Jadi, nilai f¯¹(3) yaitu -1.
Soal 7
Diketahui invers fungsi g adalah g¯¹(x) = x/(x – 1); x # 1. Jika (g o f)¯¹(x)=(-4x – 1)/(-x + 3); x # 3, rumus invers fungsi f adalah…
Jawab:
(g o f)¯¹(x)=(-4x – 1)/(-x + 3)
(f¯¹ o g¯¹)(x) = (-4x – 1) /(-x + 3)
f¯¹(g¯¹(x)) = (-4x – 1) /(-x + 3)
f¯¹(x/(x – 1)) = (-4x – 1) /(-x + 3)
Misalkan t = x/(x-1) dengan demikian:
t(x – 1) = x
tx – t = x
tx – x = t
x(t – 1) = t
x = t/(t – 1)
Maka:
f¯¹(x/(x – 1)) = (-4x – 1) /(-x + 3)
f¯¹(x) = (-5x + 1)/(2x – 3)
Jadi, rumus invers fungsi f adalah f¯¹(x) = (-5x + 1)/(2x – 3)
Soal 8
Diketahui invers fungsi g dan (f o g) berturut-turut adalah g¯¹(x) = (-x + 7)/3 dan (f o g)¯¹(x) =(27x + 11)/(12x + 6); x # -1/2, rumus fungsi f adalah…
Jawab:
-(f¯¹(x)) + 7 = (27x + 11)/(4x + 2)
(-(f¯¹(x)) + 7) (4x + 2) = 27x + 11
-4x (f¯¹(x)) – 2 (f¯¹(x)) + 7(4x) + 14 = 27x + 11
-4x (f¯¹(x)) – 2 (f¯¹(x)) + 28x + 14 = 27x + 11
-4x (f¯¹(x)) – 2 (f¯¹(x)) = -x – 3
f¯¹(x) (-4x – 2) = -x – 3
f¯¹(x) = (-x – 3)/(-4x – 2)
Misalkan y = f¯¹(x)
y = (-x – 3)/(-4x – 2)
y(-4x – 2) = -x – 3
-4xy – 2y = -x – 3
-4xy + x = 2y – 3
x(-4y + 1) = 2y – 3
x = (2y – 3)/(-4y + 1)
(f¯¹(y))¯¹ = (2y – 3)/(-4y + 1)
f(y)= (2y – 3)/(-4y + 1)
f(x) = (2x – 3)/(-4x + 1)
Jadi, rumus fungsi f adalah f(x) = (2x – 3)/(-4x + 1); x # ¼.
Soal 9
Diketahui (f o g)(x) = 2x³ – 5x² + 8x – 9. Jika g(x) = (x + 3)/2, nilai f(2) adalah…
Jawab:
(f o g)(x) = 2x³ – 5x² + 8x – 9
f(g(x)) = 2x³ – 5x² + 8x – 9
f((x + 3)/2) = 2x³ – 5x² + 8x – 9
Misalkan t = (x + 3)/2 sehingga:
2t = x + 3
x = 2t – 3
Maka,
f((x + 3)/2) = 2x³ – 5x² + 8x – 9
f(t) = 2(2t – 3)³ – 5(2t – 3)² + 8(2t – 3) – 9
f(2) = 2(2(2)-3)³ – 5(2(2)-3)² + 8(2(2)-3) – 9
f(2) = 2(4-3)³ – 5(4-3)² + 8(4-3) – 9
f(2) = 2 – 5 + 8 – 9
f(2) = -4
Jadi nilai f(2) yaitu -4.
Soal 10
Diketahui g(x) = √(4x + 5); x ≥ -5/4. Jika g¯¹(x) invers fungsi g, nilai g¯¹(1) adalah…
Jawab:
Misalkan y = g(x)
y = √(4x + 5)
Kuadratkan ruas kanan dan ruas kiri
y² = 4x + 5
4x = y² – 5
x = (y² – 5)/4
g¯¹(y) = (y² – 5)/4
g¯¹(x) = (x² – 5)/4
g¯¹(1) = (1² – 5)/4 = -4/4 = -1
Jadi, nilai g¯¹(1) yaitu -1
Soal 11
Invers fungsi g(x) = (-x + 5)/(9x – 8); x # 8/9 adalah…
Jawab:
Misalkan: y = g(x)
y = (-x + 5)/(9x – 8)
y(9x – 8) = -x + 5
9xy – 8y = -x + 5
9xy + x = 8y + 5
x(9y + 1) = 8y + 5
x = (8y + 5)/(9y + 1)
g¯¹(y) = (8y + 5)/(9y + 1)
g¯¹(x) = (8x + 5)/(9x + 1)
Jadi, invers fungsi g adalah g¯¹(x) = (8y + 5)/(9y + 1)
Soal 12
Invers dari fungsi f(x) = 2/(3x – 4) + (x – 5)/(6x – 8) adalah…
Jawab:
Misalkan y = f(x)
y = (x – 1)/(6x – 8)
y(6x – 8) = (x – 1)
6xy – 8y = x – 1
6xy – x = 8y – 1
x(6y – 1) = 8y – 1
x = (8y – 1)/(6y – 1)
f(y) = (8y – 1)/(6y – 1)
f¯¹(x) = (8x – 1)/(6x – 1)
Jadi, invers dari fungsi f adalah f¯¹(x) = (8x – 1)/(6x – 1)
Demikian “12 Soal Matematika Komposisi Fungsi dan Fungsi Invers SMA disertai Jawaban“. Semoga bermanfaat.
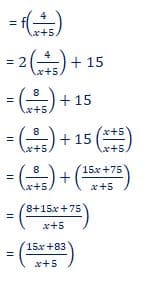
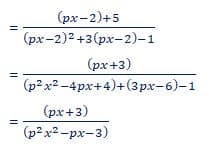
.jpg)

